![Dynamische Investitionsrechnung: Kapitalrendite]()
Neben den absoluten Kriterien wie
Kapitalwert und Endwert werden zur Beurteilung der
Vorteilhaftigkeit von
Handlungsmöglichkeiten auch Kapitalrenditen (auch
Rentabilitäten genannt) eingesetzt. Auch mit ihnen sollen Analysen durchgeführt und
Entscheidungen vorbereitet werden.
Renditen allgemein sind
relative Vorteilhaftigkeitsgrößen, weil die Zielgröße aus einem Quotienten besteht. Sie beziehen dazu einen Überschuss im Zähler entweder auf den Umsatz oder das eingesetzte Kapital. Somit sind zu unterscheiden:
- Umsatzrenditen und
- Kapitalrenditen
Diese beiden Erscheinungsformen dienen sehr unterschiedlichen Zwecken. Leider werden sie in der Praxis nicht klar auseinandergehalten. Sie können je nach Branche völlig unterschiedliche Werte annehmen, was durch ein kleines
vereinfachtes Beispiel gezeigt werden soll:
Ein
Handelsunternehmen möge eine Umsatzrendite von 2% haben, was bei einem angenommen Kapitalumschlag von 12x pro Jahr eine Kapitalrendite von 24% ergibt. Dagegen möge ein Industrieunternehmen eine Umsatzrendite von 10% aufweisen, wobei sich das Kapital aber nur 1x pro Jahr umschlägt, so dass die Kapitalrendite mit 10% viel niedriger liegt. Eine strikte Trennung zwischen Umsatz- und Kapitalrenditen ist somit notwendig. Besonders gefährlich ist die
Ebit-Rendite (besser Ebit-Umsatzrendite), welche leider in der deutschen Autoindustrie als wesentliche Kenngröße eingesetzt wird (vgl. zu den Gefahren Hoberg (2016a), S. 1029 ff.).
In diesem Beitrag geht es aber nur um die
Kapitalrenditen, und zwar aus der dynamischen Investitionsrechnung (vgl. zur
statischen Rendite). Sie geben an, um wie viel Prozent ein
Anfangskapital pro Jahr angewachsen ist (retrospektiv) bzw. anwachsen wird (prospektiv). Diese Kapitalrenditen werden insb. von Kapitalgebern eingesetzt, um zu sehen, wie erfolgreich das Unternehmen mit dem zur Verfügung gestellten Kapital gewirtschaftet hat.
Maßstab ist der
Kapitalkostensatz des Unternehmens. Dieser auch als Kalkulationszinssatz bezeichnete Mischzinssatz wird aus der
Eigen- und der
Fremdkapitalverzinsung ermittelt. Wenn der so ermittelte Kapitalkostensatz kleiner ist als die Rendite z. B. eines Projektes oder einer Handlungsmöglichkeit, so wird durch die Realisierung der Handlungsmöglichkeit Wert geschaffen. Im einfachen
einperiodigen Fall kann die Berechnung geschehen, indem der Wertzuwachs am Ende des Jahres auf den Kapitaleinsatz bezogen wird.
Beispiel:
Wenn eine
Anfangsinvestition von 500 T€
0 nach einem Jahr 600 T€
1 bringt, so ist der Wertzuwachs von 100 T€
1 im Zähler auf das eingesetzte Kapital von 500 T€
0 im Nenner zu beziehen. Die Einheiten sind für eine höhere Präzision mit einem Zeitindex versehen (vgl. hierzu Hoberg (2018), S. 468 ff.). Aus der Division von Wertzuwachs durch das eingesetzte Anfangskapital erhält man 100/500 = 0,2 = 20%. Wenn sich die Kapitalkosten auf 12% belaufen, ist die Investition bzw. die Handlungsmöglichkeit finanziell sinnvoll. Das gilt aber nur für das jeweils betrachtete
Szenario.
Das
Zeitkonzept umfasst also den Anfangszeitpunkt t = 0 und den Endzeitpunkt (hier t = tn = 1), zwischen denen dann der Wertzuwachs ermittelt wird. Hinsichtlich des eingesetzten Kapitals wird im Nenner unterschieden, ob das gesamte Kapital betrachtet wird oder nur das
Eigenkapital (vgl. z. B. Berk/deMarzo/Harford, S. 37 ff.). Dementsprechend spricht man von Gesamtkapitalrendite (ROCE Return on capital employed) bzw. Eigenkapitalrendite (ROE Return on Equity).
Und zusätzlich können beide Versionen noch vor oder nach
Ertragssteuern ermittelt werden. Wie das Einführungsbeispiel gezeigt hat, könnten Kapitalrenditen in das Produkt aus Umsatzrendite und Umschlagshäufigkeit des Kapitals zerlegt werden (siehe z. B. das
Du-Pont Modell).
Anzeige
 RS-Bilanzanalyse - Kennzahlen-Berechnung in Excel
RS-Bilanzanalyse - Kennzahlen-Berechnung in Excel
Umfangreiches Excel- Tool zur Berechnung der wichtigsten branchenunabhängigen Kennzahlen aus Bilanz und GuV. Weiterhin G+V und Bilanz in 5 Jahres-Übersicht und druckbare Berichte, die die Lage des Unternehmens im 5 Jahresvergleich darstellen.
Preis 39,- EUR inkl. MWSt.
mehr Informationen >>
Grundlagen Kapitalrenditen
Zu fragen ist, warum teilweise Kapitalrenditen (
relative Kriterien) berechnet werden sollten, wenn mit dem Kapital- und Endwert (am besten auf Basis eines vollständigen Finanzplans) sehr geeignete
absolute Kriterien zur Verfügung stehen.
Ein
Nachteil der Kapital- und Endwerte bestehen darin, dass sie zwar die Kapitalkosten über den Kapitalkostensatz berücksichtigen, aber nur wenig Auskunft darüber geben, welche Handlungsmöglichkeit(en) von vielen möglichen ausgewählt werden soll(en). Denn ein hoher Endwert ist ev. nicht so gut, wenn viel Kapital eingesetzt werden muss. Dies ist problematisch, wenn das Unternehmen nicht über ein hinreichend hohes
Investitionskapital verfügt. Denn dann sind einige Handlungsmöglichkeiten nicht realisierbar.
Dies gilt auch dann, wenn die Renditen der
abgelehnten Handlungsmöglichkeiten den Kapitalkostensatz übersteigen (sie absolut also vorteilhaft wären). Als Beispiel sei eine Rendite von 15% bei einem Kapitalkostensatz von 12% genannt. Aber wenn dann andere Handlungsmöglichkeiten eine noch höhere Kapitalrendite aufweisen, also über 15%, nutzen letztere das knappe Kapital besser ausnutzen.
Somit stellen sich die
absoluten und die
relativen Kriterien wie folgt dar:
|
Verfahrensgruppe
|
Absolute Verfahen
(Absoluter Überschuss zu einem Zeitpunkt)
|
Relative Verfahren
(Rendite r)
|
|
Beispiele
|
Endwert
Kapitalwert
Entnahmen
|
Interner Zinsfuß
Kapitalwertrate
Mod- Realverzinsung
(VoFi-Rendite)
|
|
Voraussetzungen
|
Zahlungsströme der Handlungsmöglichkeiten
|
Zahlungsströme der Handlungsmöglichkeiten
|
|
Kalkulationszinssatz i
|
benötigt
|
zunächst nicht benötigt
|
|
Vorteilhaftigkeitskriterium
|
> 0
|
Rendite r > i
|
|
Geeignet für Ermittlung der Vorteilhaftigkeit einer HM
|
ja
|
ja
|
|
Eignung für Ermittlung der Vorteilhaftigkeit vieler HMs
|
gering
|
mit Einschränkungen
|
Abb. 1: Kennzeichen absoluter und relativer Kriterien
Beide Verfahrensgruppen, die absoluten und die relativen, benötigen einen
vorbereiteten Zahlungsstrom (vgl.
Grundlagen dynamischer Investitionsrechnung). Während aber die absoluten Verfahren wie End- und Kapitalwert von einem bereits ermittelten Zinssatz zum
Auf- und Abzinsen ausgehen, ist dieser bei der internen Zinsfußmethode nicht notwendig.
Bei letzteren wird die Verzinsung ermittelt, die "intern" im Zahlungsstrom enthalten ist. Auch bei der
modifizierten Realverzinsung (am besten auf VoFi-Basis) wird aus den Zahlungen die Rendite ermittelt, wobei aber vorher Verzinsungen vorgenommen werden müssen. Für die Vorteilhaftigkeitsermittlung wird dann aber doch der Kapitalkostensatz benötig, weil er den Vergleichsmaßstab darstellt.
Für
mehrjährige Handlungsmöglichkeiten können bei der Ermittlung der Kapitalrendite allerdings einige Probleme entstehen, weil dann zu klären ist, was mit Zahlungen passiert, die nicht am Anfang in t = 0 oder Ende t = tn anfallen. Folgende wichtige Kapitalrenditen seien betrachtet:
- Einperiodige Rendite (siehe Beispiel oben)
- Interne Zinsfußmethode
- Kapitalwertrate
- (Modifizierte) Realverzinsung (sie wird häufig auf Basis Vollständiger Finanzpläne durchgeführt, weswegen sie auf VoFi-Rendite genannt werden kann.)
Immer wenn zahlreiche Handlungsmöglichkeiten um ein knappes Investitionsbudget konkurrieren, ist eine zusätzliche Anwendung der Renditekriterien zu überlegen. Viele BWL-Bücher beschäftigen sich mit der
Internen-Zinsfuß-Methode, die daher als erstes vorgestellt und diskutiert werden soll.
Die Interne-Zinsfuß-Methode
Die interne Zinsfuß-Methode hat es praktisch in alle Lehrbücher geschafft und erfreut sich auch in der Praxis großer Beliebtheit, wohl auch, weil ihre Berechnung mit einer scheinbar einfachen und problemlosen
Excel-Funktion (IKV) erfolgen kann. Der interne Zinsfuß bzw. die internen Zinsfüße ergeben sich als
Nullstellen der Kapitalwertfunktion.
Dazu muss ein
Polynom vom Grade tn gelöst werden, wobei tn die Anzahl der betrachteten Zeitpunkte darstellt. Die Gleichung kann gleichermaßen für den Endwert EW
tn oder den Kapitalwert KW
0 einer Zahlungsreihe aufgestellt werden. Hier wird die übliche Ableitung über den Kapitalwert gewählt (vgl. z. B. Wöhe, S. 494 ff., Hoberg (2023), S. 1 ff.):
|
KW0 =
|
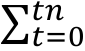
|
(EZt – AZt) × (1 + r)–t = 0
|
|
|
|
|
KW0
|
|
Kapitalwert zum Zeitpunkt 0
|
|
EZt
|
|
Einzahlungen zum Zeitpunkt t
|
|
AZt
|
|
Auszahlungen zum Zeitpunkt t
|
|
r
|
|
Interner Zinssatz
|
|
t
|
|
Zeitindex, t = 0,…,tn, üblicherweise in Jahresschritten.
|
Der Kapitalwert berechnet per
Startzeitpunkt t = 0 die Summe aller abgezinsten Zahlungen, welche durch die jeweilige Handlungsmöglichkeit im betrachteten Szenario ausgelöst würden. Wenn die Interne Zinsfußmethode zur Anwendung kommen soll, wird der Kapitalwert auf 0 gesetzt. Ein Kapitalwert von 0 bedeutet für den Investor, dass er bezüglich der Investition indifferent ist.
Bei Durchführung der Handlungsmöglichkeit erwartet er dann weder einen Nachteil noch einen Vorteil. Die gleich Null gesetzte Gleichung wird meistens mit
iterativen Verfahren nach der Rendite r aufgelöst, welche dann den Internen Zinsfuß darstellt. Vorteilhaft ist eine Handlungsmöglichkeit, wenn der Interne Zinsfuß größer ist als der Kalkulationszinssatz. Dieser muss also doch bekannt sein, so dass sich die scheinbare Einfachheit der Methode im zweiten Schritt auflöst.
Entscheidend ist zu erkennen, dass in der obigen Gleichung nur ein einziger Zinssatz, nämlich der interne Zinsfuß r, vorkommt. Somit müssen alle Verzinsungen mangels Alternative genau mit diesem Zinssatz durchgeführt werden, unabhängig davon, ob sie kurz- oder langfristig sind oder ob es sich um
Finanzierungen oder
Zwischenanlagen handelt.
Folgende
Verzinsungen können relevant werden:
- Verzinsung von kurzfristigen Anlagen im Falle von positiven Überschüssen
- Verzinsung von mittel- und langfristigen Anlagen im Falle von positiven Überschüssen (ev. auch kleine Investitionsprojekte)
- Verzinsung von kurzfristigen Krediten im Falle von negativen Überschüssen
- Verzinsung von langfristigen Krediten im Falle von negativen Überschüssen
- Verzinsung von subventionierten Krediten
- Verzinsung der gesamten Handlungsmöglichkeit
Es ist offensichtlich, dass diese
unterschiedlichen Aufgaben fast immer auch
unterschiedliche Zinssätze erfordern. Selbst wenn der Anlagenzinssatz kaum gebraucht wird (der Kreditzinssatz ist relevant, weil bei Überschüssen erst einmal Kredite zurückzuzahlen sind), so ist die Gesamtverzinsung praktisch immer abweichend von den Kreditzinssätzen.
Schon
rechentechnisch kann der Interne Zinsfuß also nicht alle Anforderungen befriedigen, weil er nicht differenzieren kann. Diese sogenannte Wiederanlageprämisse (vgl. noch genauer Hoberg (2016b), S. 789 ff.) kann zu großen Problemen führen, teilweise sogar ohne dass der Nutzer es bemerkt. Einige Probleme seien mit einem Beispiel demonstriert:
|
|
Kalkulationszinsfuß (wacc):
|
|
10%
|
|
|
|
Fall
|
Jahresendzeitpunkt
|
Interner Zinsfuß
|
Realverzinsung
|
Kapitalwert
|
Endwert
|
|
0
|
1
|
2
|
|
1
|
–1000
|
700
|
600
|
20,0%
|
17,0%
|
132,2
|
160,0
|
|
2a
|
–1000
|
2500
|
–1500
|
0,0%
|
11,8%
|
33,1
|
40,0
|
|
2b
|
–1000
|
2500
|
–1500
|
50,0%
|
11,8%
|
33,1
|
40,0
|
Abb. 2: Beispiele für Interne Zinsfüße (Quelle Hoberg (2023), S. 1 ff.)
Unter der Annahme ähnlicher Risiken der Handlungsmöglichkeiten, kann der Kapitalkostensatz (Wacc = Weighted average cost of capital) gleich sein. Im ersten Beispiel gilt für die Ermittlung des internen Zinsfußes mittels der obigen Kapitalwertwertfunktion.
KW
0 = –1000 + 700 / (1+r) + 600 / (1+r)
2 = 0
Nach
Multiplikation mit (1+r)
2 ergibt sich der Endwert EWtn zum Endzeitpunkt t = tn, der in diesem einfachen Fall 2 beträgt:
EW
tn = –1000 × (1+r)
2 + 700 × (1+r) + 600 = 0
EW
tn Endwert: Wert aller aufgezinsten Zahlungen zum Endzeitpunkt t = tn
Die Endwert-Gleichung lässt sich z. B. mittels der
p/q Formel lösen. Allerdings hat eine quadratische Funktion wie die vorliegende häufig 2 Nullstellen. Zunächst wird durch –1000 dividiert:
1 × (1+r)
2
– 0,7 × (1+r) – 0,6 = 0
(1+r) = 0,35 ± (0,35
2 + 0,6)
0,5
r
1 = 0,35 + 0,85 – 1 = 0,2 = 20%
r
2 = 0,35 - 0,85 – 1 = -1,5 = -150%
Die zweite Lösung mit –150% ist mathematisch korrekt, aber betriebswirtschaftlich nicht sinnvoll, da hohe
negative Zinssätze fast nie sinnvoll sind. Der Zinsfaktor q würde –0,5 betragen. Zudem ist eine Kapitalaufnahme zu –150% unrealistisch. Eine Vorteilhaftigkeit für Handlungsmöglichkeiten liegt nach den Renditemethoden dann vor, wenn die risikospezifischen Kapitalkosten gedeckt werden, die hier mit 10% angenommen sind. Da das Projekt 1 im betrachteten Szenario einen Internen Zinsfuß von 20% aufweist, ist es zunächst einmal vorteilhaft.
Auch die wichtige
Absicherung über positive Kapital- und Endwerte erbringt die gleiche Schlussfolgerung. Zu
problematischen Ergebnissen führen die Daten des zweiten Beispiels in Abb.2. In Fall 2a beträgt der Interne Zinsfuß 0% und scheint zu zeigen, dass das Projekt nicht vorteilhaft ist, weil der Kapitalkostensatz von 10% nicht erreicht wird. Aber die parallel berechneten Kapital- und Endwerte zeigen, dass dies ein Fehlschluss wäre. Beide sind deutlich positiv. Die interne Zinsfußmethode versagt also in dieser Zahlungsreihe.
Allerdings gibt es aufgrund der
Parabelform der Kapitalwertfunktion auch noch eine zweite Lösung mit 50% (Fall 2b). Dies ändert die Entscheidung von Ablehnung in große Vorteilhaftigkeit. Welcher Wert der richtige ist, sagt die Interne Zinsfuß Methode nicht. Während dies aufgrund der Einfachheit des Beispiels eventuell noch vom
Controller durchschaut werden kann, so kann es bei längeren Planungszeiträumen zu
Fehleinschätzungen kommen. Schwieriger wird es, wenn aus zahlreichen Handlungsmöglichkeiten die besten gerade noch finanzierbaren herausgesucht werden sollen.
Im ersten Schritt würde man vermuten, dass – ähnlich wie im
Deanmodell (vgl. z. B. Wöhe, S. 501 ff.) – diejenigen Handlungsmöglichkeiten gewählt werden, welche die höchsten Renditen aufweisen. Aber als relative Größe zeigt der Interne Zinsfuß nur die Verzinsung an, nicht aber, wie viel Kapital im Zeitablauf verzinst wird. So kann es sein, dass eine sehr rentable Handlungsmöglichkeit nach einem Jahr nur noch wenig Kapital gebunden hat und damit auch nur noch geringe Überschüsse generiert. Die negativen Internen Zinsfüße sind hier offensichtlich
betriebswirtschaftlich nicht relevant, zeigen aber nochmals die Gefahren der Internen-Zinsfuß-Methode. Da die Handlungsmöglichkeit 1 die höhere interne Verzinsung aufweist, wäre sie vorzuziehen
Kapitalwertrate
Neben der Internen Zinsfußmethode wird auch die Kapitalwertrate (vgl. z. B. Olfert, S. 113) vorgeschlagen. Sie wird teilweise als bessere Alternative zur Internen Zinsfußmethode angesehen (vgl. Becker, S. 73). Dies wäre auch für die
Praxis wichtig, weil z. B. in den USA nach einer Untersuchung 75% aller Unternehmen die – sehr umstrittene – Interne Zinsfußmethode verwenden (vgl. Berk/deMarzo/Harford, S. 218). Daher wird die Methode der
Kapitalwertrate kurz dargestellt und dann beurteilt (vgl. zu den Details mit Beispielsrechnungen Hoberg 2015b, S. 167 ff.). Zur Ermittlung der Kapitalwertrate (KWR) wird der folgende Quotient ermittelt:
Im Zähler steht der Kapitalwert KW
0, der sich dadurch ergibt, dass alle Zahlungen auf den Startzeitpunkt abgezinst werden (
Barwertbildung) und anschließend zum Kapitalwert addiert werden (siehe auch den Beitrag
Kapital- und Endwerte). Der Kapitalwert wird dann durch die Anschaffungsauszahlung A
0 dividiert. Wenn diese als negative Zahl definiert ist, so wird der absolute Betrag genommen oder mit − 1 multipliziert.
Aufgrund der Definition als Quotient handelt es sich bei der Kapitalwertrate um ein relatives Kriterium. Die Einheit €
0 Kapitalwert in t = 0 bezogen auf €
0 Anschaffungsauszahlung in t = 0 zeigt, dass die Kapitalwertrate nicht der üblichen Struktur von Renditen entspricht. Letztere fragen nach dem durchschnittlichen Wertzuwachs pro Periode (meist Jahr). Im einfachsten Fall einer einzigen Periode wird der Wertzuwachs am Ende der Periode auf die Anfangsinvestition zum Start der Periode bezogen
Beispiele Kapitalwertrate
Wenn die Anschaffungsauszahlung in t = 0 100 €
0 beträgt und der Rückfluss nach einem Jahr (in t = 1) 121 €
1, so ist zunächst der Kapitalwert zu berechnen. Bei einem Zinssatz von wieder 10% erhält man –100 + 121/1,1 = 10 €
0. Daraus ergibt sich dann die Kapitalwertrate von 10/100 = 0,1 = 10%. Bei der Kapitalwertrate sind Kapitalwert und Anschaffungsauszahlung somit auf den gleichen Startzeitpunkt bezogen. Nun sei die Rückzahlung auf 110 €
0 reduziert.
Wenn der
Kalkulationszinsfuß weiterhin 10% beträgt, so ergibt sich mit der gleichen Zahlungsreihe ein Kapitalwert von 0, der dann auch zu einer Kapitalwertrate von 0/100 = 0 % führt. Somit ist bei der Kapitalwertrate und den anderen Renditeformen nur der Zeitpunkt der Anschaffungsauszahlung identisch, nicht jedoch der Rückflusstermin. Die Interpretation der Rendite als durchschnittlicher jährlicher Wertzuwachs ist bei der Kapitalwertrate nicht möglich. Die Kapitalwertrate sei für die Daten einer
3-periodigen Handlungsmöglichkeit errechnet.
Der
Zahlungsstrom möge − 100, + 55, + 60,5, + 26,62 betragen. Im ersten Schritt wird jede einzelne Zahlung auf den Zeitpunkt t = 0 abgezinst. Aus der ersten Zahlung von + 55 €
1 in t = 1 ergibt sich beim Kalkulationszinsfuß von 10% (= 0,1) ein Zinsfaktor von (1 + 0,1) = 1,1. Durch diesen werden die 55 €
1 dividiert, was 50 €
0 per t = 0 ergibt. Die Zahlung von+ 60,5 €
2 in t = 2 wird durch 1,12 = 1,21 geteilt, was per t = 0 dann auch zu + 50 führt. Der Barwert der letzten Zahlung aus t = 3 beträgt + 26,62/1,331 = + 20 €
0.
Die Barwertsumme der Rückflüsse (teilweise
Zukunftserfolgswert genannt, siehe Wöhe, S. 514 f.) beläuft sich dann auf 120 €
0. Wenn hiervon die Anschaffungsauszahlung von 100 €0 abgezogen wird, erhält man den Kapitalwert von 20 €
0. Damit beträgt die Kapitalwertrate 20/100 = 20%. Dieses Ergebnis muss nun interpretiert werden. Allgemein gilt, dass eine Handlungsmöglichkeit vorteilhaft ist, wenn ihre Durchführung zu einer höhere Zielerreichung führt als ihre Unterlassung Konkret ist die Handlungsmöglichkeit gemäß der Kapitalwertrate dann absolut vorteilhaft, wenn sie positiv ist, also besser als die
Nullalternative (Do Nothing).
Laut Berechnungsformel geht die Anschaffungsauszahlung mit ihrem absoluten Betrag in die Formel ein. Daher entscheidet sich die Vorteilhaftigkeit über den Kapitalwert im Zähler. Ist er positiv, so ist auch die Kapitalwertrate positiv. Die Berechnung der Kapitalwertrate bringt somit für die Frage der absoluten Vorteilhaftigkeit keine zusätzlichen Informationen gegenüber dem Kapitalwertkriterium. Nun ist die relative Vorteilhaftigkeit zu prüfen. Es ist somit zu klären, ob die Kapitalwertrate als Kriterium eingesetzt werden kann, wenn zwischen verschiedenen Handlungsmöglichkeiten ausgewählt werden soll (siehe z. B. Becker, S. 73ff.).
Für die Handlungsmöglichkeiten sei angenommen, dass sie sich nicht sachlich gegenseitig ausschließen, aber sie können nicht alle durchgeführt werden, weil nicht hinreichend viel Kapital zur Verfügung steht. Das
knappe Kapital sollte dann möglichst gut genutzt werden. Dadurch dass das notwendige Anfangskapital im Nenner steht, werden Handlungsmöglichkeiten gut bewertet, wenn sie wenig Kapital benötigen. Dies ist der richtige Grundgedanke, der auch für die anderen
Renditekriterien gilt.
Es werden dann die Investitionen realisiert, welche die höchsten Renditen aufweisen. Allerdings kann eine
Reihenfolgebildung nach Maßgabe von Kapitalrenditen nur dann richtig sein, wenn die Handlungsmöglichkeiten ähnliche Risiken aufweisen. Ein Vergleich z. B. einer Finanzinvestition in ein Unternehmen mit dem Rating AAA darf nicht mit einer risikoreichen Investition verglichen werden, ohne dass die Risikounterschiede berücksichtigt werden.
Probleme der Kapitalwertrate
Die adäquate Auswahl des
Entscheidungskriteriums kann sehr wichtig für die Entscheidung sein, ob Handlungsmöglichkeiten in das Investitionsprogramm aufgenommen werden oder nicht. Insofern sollte verhindert werden, dass eher schwache Handlungsmöglichkeiten eines Geschäftsbereiches durch Anwendung eines ungeeigneten Kriteriums zu gut dargestellt werden und damit die Gefahr entsteht, dass bessere Handlungsmöglichkeiten nicht zum Zuge kommen. Hoberg hat diese Problematik für die
statische Renditevergleichsrechnung nachgewiesen (vgl. das Renditeparadoxon nach Hoberg 2013, S. 942 ff.).
Für die Kapitalwertrate besteht eine ähnliche Gefahr. Wenn Teile der Anfangsauszahlung zeitlich stark verzögert werden (z. B. durch ein Zahlungsziel von einem Jahr), dann bleibt der absolute Kapitalwert unverändert, wenn die Verschiebung mit dem gleichen Zinssatz erfolgt. Aber die Kapitalwertrate kann dann stark steigen. Die Kapitalwertrate ist also wie alle anderen Renditekriterien auch sehr anfällig gegenüber
Manipulationen der Anschaffungsauszahlung.
Ein weiteres wesentliches
Problem kann dann entstehen, wenn Handlungsmöglichkeiten mit unterschiedlichen Laufzeiten verglichen werden sollen. Es stellt sich das Problem, was mit der kürzeren Handlungsmöglichkeit passieren wird, wenn die anderen noch laufen. Die Höhe der
Wiederanlage kann ausschlaggebend für die richtige Entscheidung sein ((vgl. noch genauer Hoberg (2016b), S. 789 ff.). Bei der Kapitalwertmethode besteht die implizite Annahme, dass Überschüsse zum Kalkulationszinsfuß weiter angelegt werden (vgl. z. B. Becker, S. 79).
Da bei der Barwertbildung nun mit dem gleichen Kalkulationszinssatz abgezinst wird, ändert sich der Kapitalwert nicht, wenn z. B. die
Nutzungsdauer verlängert wird. Wenn vom absoluten Kriterium "Kapitalwert" auf das relative Kriterium der Kapitalwertrate übergegangen wird, so kann sich die Vorteilhaftigkeitsreihenfolge der betrachteten Handlungsmöglichkeiten erheblich ändern. Wenn angenommen wird, dass sich die Renditen der kürzer laufenden Handlungsmöglichkeiten wiederholen – dies entspricht der impliziten Prämisse -, so muss geprüft werden, ob wirklich solche neuen Handlungsmöglichkeiten mit ähnlicher Rendite gefunden werden können. Nimmt man jedoch der Einfachheit halber den Kalkulationszinssatz als Verzinsung für die weiteren Jahre, so wird die Kapitalrendite häufig verwässert.
VoFi-Rentabilität
Die
VoFi-Rentabilität auf Basis Vollständiger Finanzpläne (VoFis) stellt die Obermenge vieler Verfahren dar (vgl. Varnholt/Hoberg/Wilms/Lebefromm, S. 84 ff.). Hierzu gehört auch die
modifizierte Realverzinsung, welche den in der Praxis üblichen Fall abbilden kann, dass in t = 0 nicht alle Investitionsauszahlungen angefallen sind bzw. anfallen werden. Wie erwähnt kann die Vergleichbarkeit bei Renditerechnungen eingeschränkt sein, wenn die Laufzeiten und/oder die Kapitalbindungsstruktur unterschiedlich sind. Die VoFi-Rentabilität geht im Gegensatz zur Internen Zinssatzmethode hingegen von einer expliziten Angabe zur Höhe der verwendeten Zinssätze aus.
Diese bewusste Vorgehensweise ist sicherlich als wesentlich besser anzusehen. Die VoFi-Rentabilität kann weiter ausgebaut werden, indem z. B. Entnahmen im Laufe der Jahre eingegeben werden, damit der Investor schon früher von Rückflüssen profitieren kann. Dabei ist jedoch darauf zu achten, dass dann auch die
konkurrierenden Handlungsmöglichkeiten die gleichen Entnahmen bringen müssen.
Angesichts der problematischen
Wiederanlageprämisse der internen Zinssatzmethode sollte die Kalkulationen innerhalb der Laufzeit einer Handlungsmöglichkeit nicht mit dem noch gar nicht bekannten Internen Zinsfuß durchgeführt werden, sondern die Differenzen sollten mit dem Kalkulationszinsfuß bewertet werden, was in den geeigneteren Ansätzen auch so durchgeführt wird. Aber auch dieser Ansatz ist nur eine (allerdings viel bessere) Hilfslösung, weil sie zwar über die Differenzinvestitionen eine gleichmäßige rechnerische Kapitalbindung sicherstellt. Aber sie berücksichtigen nur pauschal über den Kalkulationszinsfuß, welche
alternativen Kapitalverwendungen zu den zukünftigen Zeitpunkten möglich sein werden.
Eine explizite Berücksichtigung zukünftiger Handlungsmöglichkeiten kann
methodisch sauber z. B. über eine simultane Planung geleistet werden. Diese scheitert aber regelmäßig an den Datenerfordernissen. Es soll nun die VoFi-Rentabilität in der Ausprägung der modifizierten Realverzinsung vorgestellt werden. Dazu wird bestimmt, wie viel Kapital dauerhaft im Projekt gebunden ist. Der Wert für das Beispiel beträgt 20.000 €
0. Dafür, dass der Investor für fünf Jahre diesen Betrag nicht anders einsetzen kann, erhält er am Ende einen höheren Endbetrag aus der Investition.
Die
Überschüsse, die zu den späteren Zeitpunkten anfallen, werden "angelegt" (Zeile 12). Die Anführungszeichen in der Zeile ("Geldanlage") der folgenden Tabelle sollen zeigen, dass es sich nicht um Finanzanlagen handeln kann. Rückfließendes Geld wird bei dem angenommenen
Kapitalengpass vornehmlich für weitere Handlungsmöglichkeiten verwendet oder zumindest für die Reduktion der teuersten Kredite anderer Handlungsmöglichkeiten. Auf diese Weise kumuliert sich der Endbetrag zum Ende des Planungszeitraums in t = 5 (letzte Spalte Zeile 16).
|
Zeile
|
Zeitpunkt
|
0
|
1
|
2
|
3
|
4
|
5
|
|
1
|
Zahlungen für Investition
|
–20.000
|
|
|
|
|
4.700
|
2
|
Einzahlungen
|
|
5.000
|
14.100
|
18.600
|
19.300
|
14.700
|
|
3
|
Auszahlungen
|
|
–16.000
|
–4.000
|
-5.400
|
–4.400
|
–2.100
|
|
4
|
Projekt Cash Flow
|
–20.000
|
11.000
|
10.100
|
13.200
|
14.900
|
17.300
|
|
5
|
Sollzinsen
|
|
0
|
–1.100
|
–200
|
0
|
0
|
|
6
|
Habenzinsen
|
|
0
|
0
|
0
|
1.100
|
2.700
|
|
7
|
Eingesetztes Kapital
|
20.000
|
|
|
|
|
|
|
8
|
Periodensaldo
|
0
|
–11.000
|
9.000
|
13.000
|
16.000
|
20.000
|
|
Finanzierung
|
|
|
|
|
|
|
9
|
* Kapitalaufnahme
|
0
|
11.000
|
0
|
0
|
0
|
0
|
10
|
* Kapitalrückzahlung
|
0
|
0
|
–9.000
|
–2.000
|
0
|
0
|
11
|
* Zinssatz
|
|
10,0%
|
10,0%
|
10,0%
|
10,0%
|
10,0%
|
|
"Geldanlage"
|
|
|
|
|
|
|
12
|
* Kapitalanlage
|
0
|
0
|
0
|
–11.000
|
–16.000
|
–20.000
|
13
|
* Kapitalrückfluss
|
0
|
0
|
0
|
0
|
0
|
0
|
14
|
* Zinssatz
|
|
10,0%
|
10,0%
|
10,0%
|
10,0%
|
10,0%
|
|
|
Bestandsgrößen
|
|
|
|
|
|
|
15
|
* Restfinanzierung
|
0
|
11.000
|
2.000
|
0
|
0
|
0
|
16
|
* Guthaben
|
0
|
0
|
0
|
11.000
|
27.000
|
47.000
|
Abb. 3: VoFi-Rentabilität mit Zwischenfinanzierung
Die
negativen Überschüsse, die in t = 1 kommen, werden zum Kalkulationszinssatz zwischenfinanziert. Im Beispiel sind es 11.000 €
1. Sie führen kann in den Folgejahren zu Zinsauszahlungen. Positive Überschüsse, die im Beispiel ab Zeitpunkt t = 3 anfallen, werden im Beispiel zu 10% „angelegt“. Die VoFi-Rentabilität ergibt sich nun, indem der Endbetrag (Guthaben) von 47.000 €
5 ins Verhältnis gesetzt wird zum dauerhaft gebundenen Kapital von 20.000 €
0. Es wird nun danach gefragt, mit welchem Zinssatz dieses gebundene Kapital zum Endwert "anwächst".
Mathematisch wird das Verhältnis gebildet (47.000/20.000 = 2,35) und daraus die Wurzel entsprechend der Anzahl der Perioden gezogen (hier fünf). Damit erhält man als Jahreswachstumsfaktor 1,186. Aus diesem durchschnittlichen Wachstumsfaktor wird die VoFi-Rentabilität ermittelt, indem noch 1 abzogen wird, wodurch 0,186 oder 18,6% resultiert.
Diese Kapitalrentabilität von 18,6% lässt sich nun mit den Rentabilitäten konkurrierender Handlungsmöglichkeiten vergleichen. Die Ergebnisse zeigen gut die oben beschriebenen unterschiedlichen Prämissen. Der Interne Zinsfuß geht davon aus, dass die
zwischenzeitlichen Überschüsse eben zum Internen Zinsfuß angelegt werden können (implizite Prämisse). Bei der VoFi-Rendite hingegen wird der Kalkulationszinssatz von im Beispiel 10% verwendet.
Modifizierte VoFi-Verzinsung
Im Beispiel der Abb. 3 wurde ein Kapital von 20.000 €
0 eingesetzt, was aber nicht ausreicht, um in der Anfangsphase alle
negativen Cashflows abzudecken. In t=1 muss ein Kredit über 11.000 €
1 aufgenommen werden (Zeile 9 in Abb. 3). Hier wird dem Missbrauch Tür und Tor geöffnet, weil eine Verschiebung von Teilen der Anfangsauszahlungen auf z. B. t = 1 die Rendite einiger Handlungsmöglichkeiten erhöht.
Daher wird bei der
modifizierten VoFi-Rendite die Bedingung eingeführt, dass das Anfangskapital über die gesamte Laufzeit reichen muss. Im Beispiel bedeutet dies, dass in t = 0 ein um 10.000 €
0 erhöhtes Kapital aufgenommen wird, das nach Verzinsung in t = 1 ausreicht, um den negativen Projekt
Cashflow von – 11.000 €
1. Der Saldo beträgt dann in t = 1 genau Null (siehe letzte Zeile von Abb. 4):
|
Zeile
|
Zeitpunkt
|
0
|
1
|
2
|
3
|
4
|
5
|
|
1
|
Zahlungen für Investition
|
–20.000
|
0
|
0
|
0
|
0
|
4.700
|
2
|
Einzahlungen
|
0
|
5.000
|
14.100
|
18.600
|
19.300
|
14.700
|
|
3
|
Auszahlungen
|
0
|
–16.000
|
–4.000
|
-5.400
|
–4.400
|
–2.100
|
|
4
|
Projekt Cash Flow
|
–20.000
|
11.000
|
10.100
|
13.200
|
14.900
|
17.300
|
|
5
|
Sollzinsen
|
|
0
|
0
|
0
|
0
|
0
|
|
6
|
Habenzinsen
|
|
1.000
|
0
|
1.010
|
2.431
|
4.164
|
|
7
|
Eingesetztes Kapital
|
30.000
|
|
|
|
|
|
|
8
|
Periodensaldo
|
10.000
|
–10.000
|
10.000
|
14.210
|
17.331
|
21.464
|
|
Finanzierung
|
|
|
|
|
|
|
9
|
* Kapitalaufnahme
|
0
|
0
|
0
|
0
|
0
|
0
|
10
|
* Kapitalrückzahlung
|
0
|
0
|
0
|
0
|
0
|
0
|
11
|
* Zinssatz
|
|
10,0%
|
10,0%
|
10,0%
|
10,0%
|
10,0%
|
|
"Geldanlage"
|
|
|
|
|
|
|
12
|
* Kapitalanlage
|
-10.000
|
0
|
-10.100
|
–14.210
|
–17.331
|
–21.464
|
13
|
* Kapitalrückfluss
|
0
|
10.000
|
0
|
0
|
0
|
0
|
14
|
* Zinssatz
|
|
10,0%
|
10,0%
|
10,0%
|
10,0%
|
10,0%
|
|
|
Bestandsgrößen
|
|
|
|
|
|
|
15
|
* Restfinanzierung
|
0
|
11.000
|
2.000
|
0
|
0
|
0
|
16
|
* Guthaben
|
10.000
|
0
|
10.100
|
24.310
|
41.641
|
63.105
|
Abb. 4: VoFi-Rentabilität ohne Zwischenfinanzierung
Die
Kalkulation der Kapitalrentabilität erfolgt wie im obigen Fall der Abb. 3. Der Endbetrag in Zeile 26 von 63.105 €
5 wird auf das eingesetzte Kapital von 30.000 €
0 bezogen, was einen Quotienten von 2,1035 ergibt. Nach Ziehen er fünften Wurzel und Abzug von 1 beläuft sich die Kapitalrentabilität auf 16,0%, also deutlich geringer als die 18,6% im nicht modifizierten Ansatz.
Der Grund liegt darin, dass in Abb. 3 eine
Teilfinanzierung zu 10% durchgeführt wurde, was zu einem
Leverage-Effekt (vgl. zu einem ausführlichen Beispiel Varnholt/Hoberg/Wilms/Lebefromm, S. 93 ff.). führt. Es sollten somit beide Versionen berechnet werden, um zu sehen, wie hoch der Effekt des verringerten Einsatzes von Eigenkapital sein würde.
Grenzen der (modifizierte) VoFi-Rentabilität
Es sei nochmals darauf hingewiesen, dass auch die VoFi-Rentabilität leicht angreifbar ist, weil die wichtigen Kalkulationszinssätze im Fall der Kapitalknappheit eigentlich erst dann bekannt sind, wenn die
optimale Kombination von Handlungsmöglichkeiten und Zwischenanlagemöglichkeiten bereits festgelegt wurde, was ja eigentlich Aufgabe der Rentabilitätsvergleiche war. Aber durch mehrfaches Durchrechnen mit unterschiedlichen Kalkulationszinssätzen kann der Anwender sich häufig gut einem befriedigenden Ergebnis annähern. Ansonsten wird vorgeschlagen, das Problem mit der
linearen Optimierung zu lösen. Dazu aber würden sehr viele zusätzliche Daten benötigt, so dass dies in größeren Fällen nicht praxisgerecht ist.
Schlussbetrachtung
Renditekriterien werden in der Praxis häufig eingesetzt, wobei mögliche Probleme nicht immer adäquat berücksichtigt werden, was insb. für die Interne Zinsfußmethode gilt. Richtig eingesetzt können Renditen für nützliche zusätzliche Informationen sorgen. Wichtig ist das Adjektiv "zusätzlich". Denn kein Controller sollte so leichtsinnig sein, die Vorteilhaftigkeit von Investitionen nur aufgrund von Renditen zu beurteilen. Eine Ermittlung der VoFi-Endwerte muss auf jeden Fall erfolgen. Hilfreich sind Rendite besonders dann, wenn das maximal zur Verfügung stehende Investitionskapital begrenzt ist (Situation des Kapitalmangels).
Allerdings müssen die
Problembereiche genau analysiert werden:
- Richtige Anschaffungsauszahlung: es dürfen keine Bestandteile von t = 0 auf spätere Zeitpunkte verschoben werden.
- Ähnliche Nutzungsdauer: Wenn die Nutzungsdauern zu sehr differieren, muss entschieden werden, was bei den kürzeren Handlungsmöglichkeiten nach ihrem Abschluss passieren soll.
- Die zu vergleichenden Handlungsmöglichkeiten müssen ein ähnliches Risiko aufweisen
- Anschaffungsauszahlung: Für die Frage der absoluten Vorteilhaftigkeit ist noch die Höhe der Anschaffungsauszahlung anzusprechen. Wenn die Anschaffungsauszahlungen unterschiedlich sind, wird die Frage der alternativen Verwendung der Handlungsmöglichkeit mit geringerem Investitionsbedarf relevant.
Ev.
negative Auswirkungen dieser Punkte können mit Hilfe geeigneter Differenzinvestitionen reduziert werden. Zusätzlich zu den oben genannten Problembereichen, die für alle Renditekriterien gelten, muss der Kapitalwertrate im Speziellen vorgeworfen werden, dass sie schwer zu interpretieren ist, weil Rückfluss (Kapitalwert) und Anschaffungsauszahlung auf den gleichen Zeitpunkt bezogen sind. Also sollte besser die Realverzinsung im Rahmen eines VoFis eingesetzt werden. Wenn sie in ihrer modifizierten Form verwendet wird, kann auch das Problem der
manipulierten Anschaffungsauszahlung gelöst
Literaturverzeichnis:
- Becker, H. P.: Investition und Finanzierung: Grundlagen der betrieblichen Finanzwirtschaft, 6. Aufl., Wiesbaden 2013.
- Berk, J., DeMarzo, P., Harford, J.: Fundamentals of Corporate Finance, Second Global Edition, Pearson 2012.Brealey, R., Myers, S., Marcus, A.: Fundamentals of Corporate Finance, Global Edition, 10. Edition, McGraw-Hill 2020.
- Hoberg, P.: (2016a): Jahresabschlussanalyse: Irreführende Umsatzrenditen, in: Der Betrieb, Nr. 18/2016, 69. Jg. S. 1029-1032.
- Hoberg, P.: (2016b): Wiederanlagemöglichkeiten in der Investitionsrechnung, in: Wisu 7/16, 45. Jg., S. 789-796.
- Hoberg, P. (2017): Fallen beim Internen Zinssatz vermeiden, in: Betriebswirtschaft im Blickpunkt, 8/2017, S. 215-222.
- Hoberg, P. (2018): Einheiten in der Investitionsrechnung, in: WISU, 47. Jg., 4/2018, S. 468-474. Hoberg, P. (2019): Ableitung des Kalkulationszinssatzes (Vergleichszinssatz) für die Investitionsrechnung, in: https://www.controllingportal.de/Fachinfo/Investitionsrechnung/Ableitung-des-Kalkulationszinssatzes-Vergleichszinssatzfuer-die-Investitionsrechnung.html?sphrase_id=57622044.
- Hoberg, P. (2022): Controllers Trickkiste: Renditefalle umgehen, in: https://www.controllingportal.de/Fachinfo/Investitionsrechnung/controllerstrickkiste-renditefalle-um..., 3.3.2022.
- Hoberg, P. (2023): Controllers Trickkiste: Excelfalle beim Internen Zinsfuß vermeiden, in: https://www.controllingportal.de/Fachinfo/Investitionsrechnung/controllers-trickkiste-excelfalle-beim-internen-zinsfussvermeiden.html?sphrase_id= 111149914, 25.7.2023.
- Olfert, K.: Investition, 13. Aufl., Herne 2015.
- Varnholt, N., Hoberg, P., Wilms, S., Lebefromm, U.: Betriebswirtschaftliche Grundlagen und Umsetzung mit SAP®S/4HANA, Berlin/Boston 2023.
- Wöhe, G., Döring, U., Brösel, U.: Einführung in die allgemeine Betriebswirtschaftslehre, 28. überarbeitete und aktualisierte Auflage, München 2023.
letzte Änderung P.D.P.H.
am 03.06.2025
Autor:
Prof. Dr. Peter Hoberg
|
Autor:in
 |
Herr Prof. Dr. Peter Hoberg
Professor für Betriebswirtschaftslehre an der Hochschule Worms. Seine Lehrschwerpunkte sind Kosten- und Leistungsrechnung, Investitionsrechnung, Entscheidungstheorie, Produktions- und Kostentheorie und Controlling. Prof. Hoberg schreibt auf Controlling-Portal.de regelmäßig Fachartikel, vor allem zu Kosten- und Leistungsrechnung sowie zu Investitionsrechnung.
|
|
weitere Fachbeiträge des Autors
| Forenbeiträge
|







 Über 200 Kennzahlen aus Finanzen, Personal, Logistik, Produktion, Einkauf, Vertrieb, eCommerce und IT.
Über 200 Kennzahlen aus Finanzen, Personal, Logistik, Produktion, Einkauf, Vertrieb, eCommerce und IT. Wie erstelle ich ein Tacho- oder Ampel-Diagramm? Wie kann ich Abweichungen in Tabellen ansprechend visualisieren? Das wird Ihnen hier anschaulich erklärt.
Wie erstelle ich ein Tacho- oder Ampel-Diagramm? Wie kann ich Abweichungen in Tabellen ansprechend visualisieren? Das wird Ihnen hier anschaulich erklärt.  Viel ist zum Berichtswesen oder Reporting schon geschrieben worden. Dennoch zeigen Umfragen, dass rund 50 Prozent der Empfänger von Berichten mit dem Reporting nicht zufrieden sind. Jörgen Erichsen erklärt in diesem Buch die Bedeutung und die Handhabung des Berichtswesens speziell für kleinere Betriebe. Mit zahlreichen Beschreibungen, Beispielen und Checklisten.
Viel ist zum Berichtswesen oder Reporting schon geschrieben worden. Dennoch zeigen Umfragen, dass rund 50 Prozent der Empfänger von Berichten mit dem Reporting nicht zufrieden sind. Jörgen Erichsen erklärt in diesem Buch die Bedeutung und die Handhabung des Berichtswesens speziell für kleinere Betriebe. Mit zahlreichen Beschreibungen, Beispielen und Checklisten.

 Wir, die Gubor-Gruppe, gehören als erfolgreiches, familiengeführtes Unternehmen mit rund 1.500 Mitarbeitern europaweit zu den Marktführern von Süßwarenartikeln. Unsere Produkte fertigen wir an fünf Standorten in Deutschland sowie einem Standort in Polen. Dabei setzen wir sowohl in der Beschaffung... Mehr Infos >>
Wir, die Gubor-Gruppe, gehören als erfolgreiches, familiengeführtes Unternehmen mit rund 1.500 Mitarbeitern europaweit zu den Marktführern von Süßwarenartikeln. Unsere Produkte fertigen wir an fünf Standorten in Deutschland sowie einem Standort in Polen. Dabei setzen wir sowohl in der Beschaffung... Mehr Infos >>
 Wir sind die Medizinischen Einrichtungen des Bezirks Oberpfalz. Rund 4.000 Expert:innen aus 60 Nationen arbeiten in unseren Kliniken, Pflegeheimen, Pflegeschulen oder unserem Bildungsinstitut. Wir sind spezialisiert auf die Fachgebiete Psychiatrie und Psychotherapie, Kinder- und Jugendpsychi... Mehr Infos >>
Wir sind die Medizinischen Einrichtungen des Bezirks Oberpfalz. Rund 4.000 Expert:innen aus 60 Nationen arbeiten in unseren Kliniken, Pflegeheimen, Pflegeschulen oder unserem Bildungsinstitut. Wir sind spezialisiert auf die Fachgebiete Psychiatrie und Psychotherapie, Kinder- und Jugendpsychi... Mehr Infos >>
 PlanET Biogastechnik GmbH plant, entwickelt und konstruiert Biogasanlagen für Landwirtschaft sowie Industrie im nationalen wie auch internationalen Markt. Auf unserem erfolgreichen Weg brauchen wir dich als Verstärkung. Bringe deine Ideen bei uns ein und verwirkliche dich bei uns. In unserem fami... Mehr Infos >>
PlanET Biogastechnik GmbH plant, entwickelt und konstruiert Biogasanlagen für Landwirtschaft sowie Industrie im nationalen wie auch internationalen Markt. Auf unserem erfolgreichen Weg brauchen wir dich als Verstärkung. Bringe deine Ideen bei uns ein und verwirkliche dich bei uns. In unserem fami... Mehr Infos >>
 Die Max-Planck-Gesellschaft zur Förderung der Wissenschaften e. V. (MPG) ist eine von Bund und Ländern finanzierte Selbstverwaltungsorganisation der Wissenschaft. Sie betreibt in gegenwärtig 85 Instituten und Forschungsstellen im In- und Ausland Grundlagenforschung auf natur- und geist... Mehr Infos >>
Die Max-Planck-Gesellschaft zur Förderung der Wissenschaften e. V. (MPG) ist eine von Bund und Ländern finanzierte Selbstverwaltungsorganisation der Wissenschaft. Sie betreibt in gegenwärtig 85 Instituten und Forschungsstellen im In- und Ausland Grundlagenforschung auf natur- und geist... Mehr Infos >>
 Seit 1930 steht die Ulmer Wohnungs- und Siedlungs-Gesellschaft mbH für bezahlbares Wohnen in Ulm. In den mehr als 95 Jahren haben wir uns zum größten lokalen Mietwohnungsanbieter entwickelt – mit über 7.500 Wohnungen geben wir zahlreichen Ulmerinnen und Ulmern aus unterschiedlichen Gesellschaftss... Mehr Infos >>
Seit 1930 steht die Ulmer Wohnungs- und Siedlungs-Gesellschaft mbH für bezahlbares Wohnen in Ulm. In den mehr als 95 Jahren haben wir uns zum größten lokalen Mietwohnungsanbieter entwickelt – mit über 7.500 Wohnungen geben wir zahlreichen Ulmerinnen und Ulmern aus unterschiedlichen Gesellschaftss... Mehr Infos >>
 Wir sind ein führender System- und Lösungsanbieter der industriellen Sensor- und Automatisierungstechnik mit Headquarters in Fulda. Weltweit erzielen wir einen Jahresumsatz von über 300 Mio. Euro. Was uns auszeichnet, ist die Verbindung zwischen Tradition und Innovation. Als Familienunternehmen a... Mehr Infos >>
Wir sind ein führender System- und Lösungsanbieter der industriellen Sensor- und Automatisierungstechnik mit Headquarters in Fulda. Weltweit erzielen wir einen Jahresumsatz von über 300 Mio. Euro. Was uns auszeichnet, ist die Verbindung zwischen Tradition und Innovation. Als Familienunternehmen a... Mehr Infos >>
 Wir von Hedin Automotive haben es uns zum Ziel gemacht, fester Teil der Mobilität von morgen zu werden. Die Herausforderungen dabei meistern wir tagtäglich im Team. Und zwar als einer von Deutschlands größten Handelspartnern von Mercedes-Benz, Daimler Truck und Hyundai mit über 30 Standorten. Uns... Mehr Infos >>
Wir von Hedin Automotive haben es uns zum Ziel gemacht, fester Teil der Mobilität von morgen zu werden. Die Herausforderungen dabei meistern wir tagtäglich im Team. Und zwar als einer von Deutschlands größten Handelspartnern von Mercedes-Benz, Daimler Truck und Hyundai mit über 30 Standorten. Uns... Mehr Infos >>
 Berlin gemeinsam besser, grüner und sauberer machen – das ist unsere Mission als größtes kommunales Entsorgungsunternehmen Deutschlands. Dafür suchen wir engagierte Persönlichkeiten. Für unseren Geschäftsbereich Controlling / Finanz- und Rechnungswesen suchen wir am Standort Ringbahnstraße befris... Mehr Infos >>
Berlin gemeinsam besser, grüner und sauberer machen – das ist unsere Mission als größtes kommunales Entsorgungsunternehmen Deutschlands. Dafür suchen wir engagierte Persönlichkeiten. Für unseren Geschäftsbereich Controlling / Finanz- und Rechnungswesen suchen wir am Standort Ringbahnstraße befris... Mehr Infos >>








 Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>
Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>