Controllers Trickkiste: Vorzeichenprobleme entschärfen

In wirtschaftlichen Analysen muss der Controller in Erfahrung bringen, in welche Richtung sich eine abhängige Größe entwickelt, wenn sich eine unabhängige verändert. Als einfaches Beispiel sei eine Preiserhöhung betrachtet. Mittels der Elastizität (Details weiter unten) kann der Controller abschätzen, wie die Mengen wohl auf Preisänderungen reagieren werden.

Ganz wichtig ist dabei das Vorzeichen, was in diesem Fall bei richtiger Anwendung fast immer negative Werte aufweist. Wenn die Elastizität z. B. –2 beträgt, so führen Preiserhöhungen zu Absatzrückgängen.

Im Beispiel sinkt die Nachfrage um 2 % für einen Prozentpunkt Preiserhöhung. In seltenen Fällen kann die Menge jedoch auch steigen, so dass die Elastizität positive Werte annimmt. Die Art des Vorzeichens ist somit außerordentlich wichtig. Darin darf sich der Controller nicht irren.

Leider aber gibt es nicht nur in diesem Fall die Konvention, die Zahlen zur angeblich besseren Verständlichkeit positiv darzustellen, so dass der grundsätzliche Zusammenhang ins Gegenteil verdreht wird. Dies wird für Elastizitäten, die häufig diskutieren Gender Pay Gaps und auch für Reportingprobleme untersucht.

1. Verkehrtes Vorzeichen bei Elastizitäten

Auch durch die hohe Inflation sahen sich Unternehmen immer wieder gezwungen, ihre Preise anzuheben. Unklar war das Ausmaß der Erhöhungen.

Um die optimale Erhöhung herauszufinden, schätzt die Marktforschung die sogenannte Nachfrageelastizität in Bezug auf Preisänderungen (vgl. z. B. Wöhe, S. 406 ff.). Zunächst ohne Berücksichtigung von Preisschwellen wird versucht, die Reaktion der Konsumenten zu schätzen, was nicht einfach ist, weil auch die Reaktion der Konkurrenten antizipiert werden muss (vgl. Hoberg (2017), S. 30 f.).

Im Standardmodell (vgl. z. B. Wöhe, S. 407 ff.) wird eine lineare Preis–Absatzfunktion angenommen:

p_N = p_PH + a × x in GE/ME

p_N – Nettopreis in GE/ME
a – Steigungsparameter, üblicherweise negativ, in GE/(ME/Pe)
x – Fakturierte Menge in Mengeneinheiten in der betrachteten Periode (ME/Pe)

Für die Nutzung dieses Standardmodells sind einige Präzisierungen notwendig. Insbesondere sei darauf hingewiesen, dass der Preis immer der Nettopreis sein muss, also nach Berücksichtigung aller Rabatte (in der Rechnung, auf den Rechnungsbetrag und Rückvergütungen) und der Effekte der Zahlungsziele (vgl. Varnholt/Lebefromm/Hoberg, S. 126–128). In der Literatur wird dies als "price waterfall" bezeichnet (vgl. Vohra/Krishnamurthi, S. 74 ff.), wobei in der Realität noch mehr Erlösreduktionen anfallen.

Es fehlen z. B. die Effekte von Zahlungszielen und die von subventionierten Krediten. Auf weitere Probleme der Preis–Absatzfunktion wird hier nicht eingegangen, weil sie für das Thema nicht relevant sind (vgl. zu den Schwierigkeiten Hoberg (2018), S. 1937 ff.). Ein Beispiel möge die Anwendung der linearen Preis–Absatzfunktion zeigen. Dafür sei ein Prohibitivpreis von 100 €/ME und eine negative Steigung von –0,1 €/(ME/Pe) angenommen, so das sie wie folgt aussieht:

p_N = 100 – 0,1 × x in €/ME

Beim Prohibitivpreis von p_PH = 100 €/ME ist laut dieser Preisabsatzfunktion ein Preisniveau erreicht, bei dem auch der größte Fan des untersuchten Produktes nicht mehr kauft. Für jede Mengeneinheit, die das Unternehmen nun (mehr) verkaufen will, muss es den Nettopreis jeweils um 0,1 €/ME reduzieren. Daher das negative Vorzeichen. Bei der obigen Formel wurde die übliche Schreibweise angewendet mit x als unabhängiger Variable. Dies ist nicht richtig, weil der Preis die Menge bestimmt.

Daher muss die Formel nach x aufgelöst werden:

x	=	(100 – pN)	= 1000 – 10	× pN in ME/Pe
		0,1

Die Menge wird in Mengeneinheiten in der betrachteten Periode gemessen (ME/Pe). Bei einem Preis von 50 €/ME ergibt sich eine Menge von 1000 – 10 × 50 = 500 ME/Pe. Bei den gewählten Parametern lassen höhere Preise die Menge schrumpfen, niedrigere lassen sie steigen.

Wenn die Preis–Absatzfunktion bekannt ist, kann die Elastizität η wie folgt geschrieben werden:

η_x,p = dx/x / dp_N / p_N = dx / dp_N × p_N / x

η_x,p – Nachfrageelastizität der Menge x in Bezug auf den Preis p_N

Die relative Mengenänderung dx / x wird auf die sie verursachende relative Preisänderung dp_N / p_N bezogen. Dabei kürzen sich die Einheiten heraus. Für das Beispiel mit p_N = 50 und x = 500 erhält man die folgende Elastizität:

ηx,p	=	dx	×	pN	= –10	×	50	= –5
		dpN		x			100

dx/dp_N – Ableitung der Mengenfunktion nach dem Nettopreis

Dieser Wert gilt nur für die betrachtete Preismengenkombination. Die Nachfrage reagiert somit bei einem Preis über 50 €/ME sehr empfindlich auf Preissteigerungen. Bei einem Prozent Preiserhöhung beträgt die Mengenänderung –5 %. Sie fällt also um 5 %. Wichtig ist nun das negative Vorzeichen.

Wenn zu dessen Vermeidung die Formel wie bei Wöhe zur "einfacheren Handhabung" (S. 406) mit –1 multipliziert wird, so ist nicht mehr sofort zu erkennen, in welche Richtung sich die Änderungen bewegen werden. Das Vorzeichen ist also im wahrsten Sinne des Wortes "verkehrt".

Das verkehrte Vorzeichen wird besonders problematisch, wenn man an die wenigen Ausnahmen denkt, in denen eine Preiserhöhung zu mehr Menge führt, z. B. durch den Snob–Effekt. Dann wäre die Elastizität nach herkömmlicher Schreibweise negativ, obwohl ein positiver Zusammenhang vorliegt.

2. Verkehrte Vorzeichen im Gender Pay Gap

Zumindest einmal pro Jahr wird der Gender Pay Gap besonders diskutiert. Er soll zeigen, inwieweit Frauen durchschnittlich schlechter entlohnt werden als Männer. Diese Benachteiligung von Frauen verstößt gegen das Allgemeine Gleichbehandlungsgesetzes (AGG).

Gleich in Paragraph 1 wird bestimmt, dass

"Benachteiligungen aus Gründen der Rasse oder wegen der ethnischen Herkunft, des Geschlechts, der Religion oder Weltanschauung, einer Behinderung, des Alters oder der sexuellen Identität zu verhindern oder zu beseitigen"

sind. Diese Vorschrift ist auch von Unternehmen einzuhalten. Ein Verstoß kann für die Unternehmen teuer werden, wenn eine Ungleichbehandlung nachgewiesen werden kann.

Ein Teil der Lohn–Differenz lässt sich durch Bereinigungen eliminieren, die sich z. B. auf Unterschiede in den folgenden Faktoren zurückführen lassen:

1. Qualifikation (z. B. höchster Bildungsabschluss)
2. Berufs/Branchenwahl (Frauenanteil in gut bezahlten Berufen geringer)
3. Erwerbsbiographie (welche Erfahrungen wurden angehäuft)

Als Beispiel für b) sei aufgeführt, dass Frauen häufiger Berufe wählen, die schlechter bezahlt werden (z. B. Kindergärtnerin statt Handwerker). Laut Destatis (siehe Link im Literaturverzeichnis) betrug der Unterschied im Jahre 2022 unbereinigt 18% und bereinigt 7%, was dann als Obergrenze zu verstehen ist, weil es noch weitere sachlich nachvollziehbare Gründe für eine Nicht–Gleichbehandlung geben kann.

Bei dieser wichtigen Fragestellung sollte im ersten Schritt geklärt werden, was überhaupt gemessen wird bzw. werden soll. Die angewendete Formel für den Gender Pay Gap (GPG) lautet nach Destatis:

GPG	=	(DSLM – DSLF)
		DSLM

DSL_M – Durchschnittlicher Stundenlohn Männer (Frauen bei Index F)

In dieser offiziellen Formel werden also durchschnittliche Stundenlöhne ausgewiesen, um unterschiedliche Höhe der Wochenarbeitszeiten ausgleichen zu können. Die Differenz – gleich Mehrbezahlung der Männer in der Mehrzahl der Fälle – wird dabei laut der obigen offiziellen Formel auf den Stundenlohn der Männer bezogen.

Für 2022 hat Destatis die folgenden Werte ermittelt. Der durchschnittliche Stundenlohn im unbereinigten Fall lag für die Männer bei 24,36 €/h und für Frauen bei 20,05. Der absolute Gap betrug somit 4,31 €/h. Laut der offiziellen (problematischen) Formel erhält man damit den folgenden relativen Wert (vgl. Destatis):

GPG2022	=	(24,36 – 20,05)	= 18 %
		24,36

Der Gap ist laut der Formel somit positiv, was natürlich nicht sein kann, weil Frauen im Durchschnitt ja geringer entlohnt werden. Eine kleine Skizze möge die Zusammenhänge deutlich machen.


Abb. 1: Bestandteile Gender Pay Gap (Stundenlohn Mann = 100)

Unbereinigt erhalten Frauen laut Destatis durchschnittlich 82,3 % der Stundenverdienste der Männer. Ca. 10 %–Punkte der Differenz von 17,7 Prozentpunkten sind laut Destatis durch Bereinigungen hinsichtlich Qualifikation, Art der Tätigkeit und Erwerbsbiographie erklärbar.

Weitere denkbare Bereinigungen sind in Abb. 1 mit der Risikoneigung und auch mit unbezahlten Überstunden aufgeführt, aber noch nicht quantifiziert. Insofern ist nicht exakt zu bestimmen, wie hoch letztendlich der Rest ist, der u.a. auf Diskriminierung zurückzuführen ist.

Da die Differenz der durchschnittlichen Stundenlöhne (DSLM – DSLF) gemäß der offiziellen Formel auf den durchschnittlichen männlichen Stundenlohn im Nenner bezogen wird, ist der absolute Gap somit positiv, solange der Mann mehr erhält. Dies ist in den meisten Vergleichsgruppen der Fall. Wenn die Formel akzeptiert wird, soll somit mit einer positiven Differenz der Nachteil der Frauen gezeigt werden…

Für sinnvolle Analysen sollte entweder der Mehrverdienst der Männer oder der Minderverdienst der Frauen analysiert werden. Beide Ansätze lassen sich aus der obigen Abb. 1 ableiten. Zusätzlich ist zu entscheiden, ob die absolute oder die relative Differenz gezeigt und ausgewertet werden soll.

Damit gibt es gemäß Abb. 2 die folgenden 4 sinnvollen Möglichkeiten:


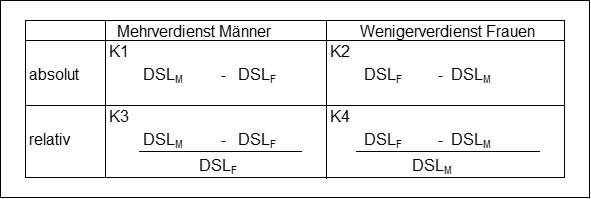Abb. 2: Sinnvolle Definitionen für den Gender Pay Gap

Unter den sinnvollen Ansätzen findet sich nicht die von Destatis verwendete Formel. Am einfachsten zu interpretieren ist wohl der relative Mehrverdienst der Männer (Kasten K3 in Abb. 2), eine positive Prozentzahl.

Alternativ könnte man die relative Lohnlücke der Frauen betrachten (Kasten K4), die im Normalfall selbstverständlich ein negatives Vorzeichen haben muss. Mit den von Destatis für das Jahr 2022 erhobenen durchschnittlichen Stundenlöhnen der Männer von DSLM = 24,36 €/h und der Frauen von DSLF = 20,05 €/h ergibt sich:

Ansatz:	Mehrverdienst Männer	Wenigerverdienst Frauen
absolut in €/h	4,31	–4,31
relativ	21,5 %	–17,7 %

Tabelle 1: Absolute und relative Gender Pay Gaps auf Basis der Durchschnittsdaten

Die in Tabelle 1 nun korrekt definierten Unterschiede – Männer bekommen unbereinigt 21,5 % mehr als Frauen oder Frauen haben einen Abstand von –17,7% im Vergleich zu den Männern – sind entweder zu erklären oder abzubauen: Dies ist aber nicht mehr das Thema dieses Beitrages. In jedem Fall sollte das Vorzeichen den Weg weisen, was auch umgekehrt gilt, wenn in bestimmten Gruppen (z. B. Vorständinnen) die Frauen mehr verdienen. Gleiches gilt übrigens auch für die Gender Pension Gaps.

3. Irreführendes Vorzeichen im Reporting

Auch in der Finanzberichterstattung (Reporting) findet man teilweise problematische Vorzeichen. Dies kann bei prozentualen Veränderungen geschehen, wenn die Bezugsgröße im Nenner negativ ist. Die prozentuale Änderung PÄ ist wie folgt definiert (vgl. Hoberg (2020), S. 1 ff.):

PÄ	=	NW	–1
		AW

NW – Neuer Wert
AW – Alter Wert (Bezugsgröße)

Wenn nach einem Ergebnis von –10 Mio€₀ im alten Jahr (Bezugsgröße) im Folgejahr ein Ergebnis von –20 Mio€₁ erzielt wird, ergibt sich die folgende Veränderungsrate:

PÄ	=	–20	=	2 – 1 = 1 = 100 %
		–10 – 1

Die negativen Vorzeichen kürzen sich somit heraus, so dass eine positive Veränderung resultiert, die hier aber sagen müsste, dass der Verlust verdoppelt wurde. Eine solche Verlustverdopplung würde also sehr positiv ausgewiesen, wenn der Controller nicht aufpasst.

Ähnlich sieht es aus, wenn auf ein Jahr mit negativem Ergebnis ein positives folgt. Wenn die Bezugsgröße wieder –10 Mio€₀ beträgt und die des Folgejahres 5 Mio€₁ – also positiv – , erhält man die folgende prozentuale Änderung PÄ₂:

PÄ2	=	+5	=	–0,5 – 1 = –1,5 = –150 %
		–10 – 1

Die Änderung weist einen negativen Wert auf, was nicht der erfreulichen Tatsache der Rückkehr in die schwarzen Zahlen entspricht.

4. Schlussbetrachtung

Bei den Elastizitäten, den Gender Pay Gaps und auch im Reporting haben sich leider falsche Schreibweisen hinsichtlich der Vorzeichen eingebürgert. Die angestrebte Vereinfachung durch das Ausweisen positiver Werte (per Multiplikation mit –1) öffnet Tür und Tor für Irrtümer. Insb. der Controller muss aufpassen, dass er sich nicht von den falschen Vorzeichen in die Irre führen lässt.

Er sollte somit sein besonderes Augenmerk darauf lenken, ob die untersuchten Größen positiv oder negativ auf Änderungen der verursachenden Größen reagieren.



Literatur:

• Destatis: Gender Pay Gap 2022, in: https://www.destatis.de/DE/Presse/Pressemitteilungen/2023/01/PD23_036_621.html.
• Hoberg, P. (2013): Elastizitäten und Preispolitik, in Wisu 3/2013, 42. Jg., S. 320–326.
• Hoberg, P. (2017): Controllers Trickkiste: Antizipative Marktanalyse, in: Controlling–Journal 5/2017, S. 30–31.
• Hoberg, P. (2018): Gewinnoptimierung mit realistischen Preisabsatzfunktionen in: Der Betrieb, 71. Jg., 33/2018, S. 1937–1941.
• Hoberg, P. (2020): Controllers Trickkiste: Denkfehler in der Prozentrechnung aufdecken, in: https://www.controllingportal.de/Fachinfo/Grundlagen/Controllers-Trickkiste-Denkfehler-in-der-Prozentrechnung-aufdecken.html, 7.8.2020, Update 27.3.2023.
• Wöhe, G., Döring, U.: Einführung in die Allgemeine Betriebswirtschaftslehre, 27. Auflage, München 2020.

letzte Änderung P.D.P.H. am 03.06.2025 Autor:  Prof. Dr. Peter Hoberg

Autor:in

	Herr Prof. Dr. Peter Hoberg Professor für Betriebswirtschaftslehre an der Hochschule Worms. Seine Lehrschwerpunkte sind Kosten- und Leistungsrechnung, Investitionsrechnung, Entscheidungstheorie, Produktions- und Kostentheorie und Controlling. Prof. Hoberg schreibt auf Controlling-Portal.de regelmäßig Fachartikel, vor allem zu Kosten- und Leistungsrechnung sowie zu Investitionsrechnung.
weitere Fachbeiträge des Autors | Forenbeiträge