Home / Fachinfo / Kostenrechnung

Controllers Trickkiste: Umrechnungen zwischen Jahres- und Monatsraten

Dr. Peter Hoberg
 

Unternehmen und auch Privatleute haben in einigen Fällen die Möglichkeit, zwischen monatlicher und jährlicher Zahlungsweise zu wählen. Dies gilt z.B. für Versicherungsbeiträge, bei denen die Versicherungsunternehmen von jährlich vorschüssiger Zahlung ausgehen, aber gegen Aufpreis auch monatliche Zahlungen akzeptieren. Der Versicherungsnehmer muss also berechnen, was für ihn besser ist. Dabei muss er auch berücksichtigen, ob die Jahres- bzw. Monatsraten jeweils vorschüssig (Monats- bzw. Jahresanfang) oder nachschüssig (Monats- bzw. Jahresende) anfallen.

Auch im Einkauf kann manchmal entschieden werden, ob der Jahresbedarf sofort bezahlt wird oder in vor- oder nachschüssigen Monatsraten. Je früher bezahlt wird, um so besser ist es für den Zahlungsempfänger. Daher müssen die Zinseffekte bei den Umrechnungen berücksichtigt werden. Dies wird im Folgenden näher ausgeführt, wobei auf eine präzise Darstellung der Zeitpunkte geachtet wird.

1. Grundlagen

Eine jegliche zeitliche Verschiebung von Zahlungen führt zu Zinseffekten, die hinsichtlich ihrer Vorteilhaftigkeit zu beurteilen sind. Zur Bewertung wird ein Zinssatz benötigt, der als Mischzinssatz von Eigen- und Fremdkapital abzuleiten ist. Im Englischen heißt er Weighted Average Cost of Capital (Wacc). Je nach Einsatzzweck erfolgt eine unterschiedliche Gewichtung der Eigen- und Fremdkapitalanteile.

Für die folgenden Beispiele sei der Wacc mit 0,5 Prozent pro Monat angenommen, was 1,00512–1 = 6,168 Prozent pro Jahr entspricht. Es sei darauf hingewiesen, dass die Zinssätze auch mit Einheiten versehen werden können. Wenn t als Monatsindex definiert wird, ist die Einheit des Monatszinssatzes €t+1 / €t. Für jeden Euro, der in t investiert wird, erhält man 0,5 % Zinsen in t+1 zurück..

Wenn der Zinssatz richtig gewählt wurde, dann ist der Entscheidungsträger indifferent, ob er in t=0 100 €0 erhält oder in t=1 100,50 €1. Allgemein ausgedrückt bedeutet dies: 100 €t  in t oder 100 * 1,005∆t €t+∆t. in t+∆t. Es handelt sich dann um äquivalente Transformationen. Wenn Monatsraten mit diesen Zinssätzen auf das Jahresende hochgezinst werden, so entsteht eine Gleichwertigkeit zwischen den Monatsraten und der Einmalzahlung am Jahresende.

Dies möge das folgende Beispiel zeigen. Gegeben seien Monatsraten von je 1000 €, und zwar einmal vorschüssig 1000 €0;11 und einmal nachschüssig 1000 €1;12. Ihr jeweiliger Wert soll per Jahresanfang ermittelt werden. Dies entspricht der Fragestellung, wie Monatsraten durch eine Einmalzahlung am Jahresanfang abgelöst werden können. Um eine Gleichwertigkeit zu erzielen, muss jede Monatsrate entsprechend ihrem Abstand auf den Jahresanfang abgezinst werden, was in Abb. 1 durchgeführt ist.

Letzte Änderung W.V.R am 01.06.2025

Autor(en): Dr. Peter Hoberg
Für Premium-Mitglieder frei Login zum Weiterlesen Mitglied werden

Bleiben Sie auf dem Laufenden mit unserem Newsletter

Tragen Sie sich für den kostenfreien und unverbindlichen Newsletter von Controlling-Portal.de ein und erhalten Sie jeden Monat aktuelle Neuigkeiten für Controller. Wir informieren Sie über neue Fachartikel, über wichtige News, aktuelle Stellenangebote, interessante Tagungen und Seminare. Wir empfehlen Ihnen spannende Bücher und geben Ihnen nützliche Excel-Tipps. Verpassen Sie nie mehr wichtige Diskussionen im Forum und stöbern Sie in Software-Angeboten, die Ihnen den Arbeitsalltag erleichtern. Beispiel-Newsletter >>

Jetzt Newsletter gratis erhalten

Premium-Stellenanzeigen



Eigenen Fachbeitrag veröffentlichen? 

Sie sind Autor einer Fachpublikation oder Entwickler einer Excel-Vorlage? Gern können Sie sich an der Gestaltung der Inhalte unserer Fachportale beteiligen! Wir bieten die Möglichkeit Ihre Fachpublikation (Fachbeitrag, eBook, Diplomarbeit, Checkliste, Studie, Berichtsvorlage ...) bzw. Excel-Vorlage auf unseren Fachportalen zu veröffentlichen bzw. ggf. auch zu vermarkten. Mehr Infos >>

Kommentar zum Fachbeitrag abgeben

Nur registrierte Benutzer können Kommentare posten!

Controlling- Newsletter

Neben aktuellen Fach- und Arbeitsmarkt-Trends für Controller und neu eingegangene Fachbeiträge, informieren wir Sie über interessante Veranstaltungen und stellen Ihnen einzelne Controlling-Tools im Detail vor.
Werden Sie jetzt monatlich über neue Fachbeiträge, Jobs und Tools informiert! 
Zur Newsletter-Anmeldung >>

Über 3.000 Artikel und Vorlagen

Community_Home.jpg






Werden Sie Mitglied in einer großen Controller-Community (über 12.000 Mitglieder!) und erhalten Zugriff auf viele Inhalte und diskutieren ihre Fragen im Controlling-Forum.

Sehen Sie hier die neuesten Fachbeiträge >>
Anzeige

Eine neue Stelle?

Mit dem Studium fertig, Umzug in eine andere Region, Aufstiegschancen nutzen oder einfach nur ein Tapetenwechsel? Dann finden Sie hier viele aktuell offene Stellen im Controlling.
Zu den Stellenanzeigen >>

Zukunft_Aussicht_Menschen_Fernglas_pm_prometeus_315.jpg

Sie suchen einen Controller? Mit einer Stellenanzeige auf Controlling-Portal.de erreichen Sie viele Fachkräfte. weitere Informationen >>

Controller- Stellenmarkt

Buchhalter Immobilien (m/w/d) – Schwerpunkt Mieten- und Objektbuchhaltung, Strohauer Wohnungsunternehmen GbR, Berlin
Leitung Controlling Finanzen (m/w/d), DRK-Blutspendedienst Baden-Württemberg – Hessen gGmbH, Mannheim
Financial Controller (m/w/d), Smurfit Westrock GmbH Werk Rheinwelle, Kreuzau
Steuerberater/in- Steuerfachwirt/in (m/w/d), Captain´s Schnitzel, Rostock
Werkscontroller (m/w/d), Kässbohrer Geländefahrzeug AG, Laupheim
Mitarbeiter*in für die Debitorenbuchhaltung, Hochschule Osnabrück, Osnabrück
Controller (m/w/d) für Förder- und Innovationsprojekte, Siltronic AG, Burghausen, München
Sachbearbeiter*in Buchhaltung in Voll- oder Teilzeit, Max-Planck-Institut für medizinische Forschung, Heidelberg

Alle Einträge Neuer Eintrag

KLR-Begriffe von A bis Z

A-C   D-F   G-I   J-L   M-R   S-U   V-Z 

Testen Sie ihr Wissen mit unseren Aufgaben und Lösungen im Bereich Kostenrechnung >>

Sie haben eine Frage?

Ratlos_Verwirrt_pm_RainerPlendl_400x275.jpg

Nutzen Sie kostenfrei das Forum für Controller und und diskutieren ihre Fragen zu Controlling-Themen.

Controlling-Software

BusinessPlanner* - Software für Finanzplanung
Jedox
Lucanet Konsolidierungssoftware
Lucanet Finanzplanungssoftware
Diamant/4 Rechnungswesen und Controlling
Serviceware Performance
Alle Einträge Neuer Eintrag

Riesen- Ressource

Auf Controlling-Portal.de sind bereits über 1.800 Fachbeiträge veröffentlicht und ständig kommen neue dazu.

Zu den neuesten Fachbeiträgen >>
Zu den derzeit meistgelesenen Fachbeiträgen >>
Zu den Premium-Beiträgen >>

Sie möchten auch einen Fachbeitrag hier veröffentlichen? Dann erhalten Sie hier weitere Informationen >>

Neueste Excel-Vorlagen

Excel-Tool: RS Bilanzanalyse (Kennzahlen Berechnung)
RS Anlagenverwaltung - Anlagenübersicht und Abschreibungen berechnen
CAPEX-Cockpit – Investitionsrechnung in Excel HGB-konform mit NPV, IRR, AfA, DATEV-Buchungssatz & GF-Vorlage
Verpflegungsmehraufwendungen 2025- Excel-Vorlage
Jahresabschluss-Cockpit HGB – Bilanzanalyse mit KI-Prompt & Altman Z-Score
Excel-Arbeitshilfe: Kapitalbedarfsplanung und Finanzierungsmix
Excel Arbeitshilfe: Optimale Bestellmenge berechnen
Betriebskostenabrechnung / Nebenkostenabrechnung Mietwohnungen
WACC-Rechner in Excel
Excel-Vorlage zum Evaluieren einer Immobilien-Investition
Alle Einträge Neuer Eintrag

Amüsante Glosse

Zweifel_Denken_Frau_Brille_pm_luckyraccoon_400x300.jpg

Erfolgreiche Unternehmer einer Kleinstadt treffen sich regelmäßig im örtlichen Golfclub und diskutieren mit Ihrer Lieblingskellnerin und BWL-Studentin Pauline betriebswirtschaftliche Probleme. Amüsant und mit aktuellem Bezug geschrieben von Prof. Peter Hoberg.

Zur Serie "Neulich im Golfclub" >>

News

Fachkräftemangel im Finanz- und Rechnungswesen – Ursachen und Auswege
Effiziente Unternehmenssteuerung im Anlagenbau mit vollumfänglicher Transparenz
Künstliche Intelligenz im Finanz-Cockpit: Agenten übernehmen, Menschen entscheiden
Im Schnitt 4 Monate auf Jobsuche: Hochschulabsolvent*innen erleben Realitätsschock
Rechnungsverarbeitung im Kontext der Public Cloud
Digitalisierungs­aktivitäten im Mittelstand verlieren deutlich an Schwung
Stärker digitalisierte Unternehmen weisen eine höhere Produktivität auf
Künstliche Intelligenz beschleunigt digitale Transformation im Rechnungswesen

Sie möchten sich weiterbilden?

mann-treppe-up-karriere_pm_pressmaster_B10716345_400x300.jpg

In unserer Seminar-Rubrik haben wir einige aktuelle Seminar- und Kurs-Angebote für Controller, u.a. auch Kurse zum Controller / IHK zusammengestellt.

Premium-Mitgliedschaft

Erhalten Sie Zugriff auf Premium-Inhalte von Controlling-Portal.de und Rechnungswesen-Portal.de. Aktuelle und ständig erweiterte Fachbeiträge. Verschaffen Sie sich hier einen Überblick über unsere Premium-Inhalte.

Mitgliedschaft für nur 39,- EUR einmalig bei unbegrenzter Laufzeit! Kein Abonnement! Weitere Informationen >>
 

Wie zufrieden sind Sie mit uns?

Über Ihre Meinung und auch ihre Anregungen für Veränderungen oder Erweiterungen würden wir uns sehr freuen. Nur 10 kurze Fragen, die schnell beantwortet sind. Vielen Dank im Voraus für Ihre Mithilfe! zur Umfrage >>
 

Jobletter und Newsletter!

Mit dem monatlich erscheinenden Newsletter werden Sie über neue Fachbeiträge, News und Excel-Tools informiert! zur Anmeldung >>

Der 14-tägige Jobletter informiert Sie automatisch über neue Stellenangebote und Arbeitsmarkt-News! zur Anmeldung >>
 

Fachbeitrag veröffentlichen?

Sie sind Autor von Fachbeiträgen mit Controlling-bzw. Rechnungswesen-Thema? Gerne veröffentlichen oder vermarkten wir ihren Fachbeitrag. Eine kurze Autorenvorstellung oder Unternehmensdarstellung am Ende des Artikels ist möglich. jetzt Mitmachen >>

Talentpool - Jobwechsel einfach!

HR-Bewerbung-Digital_pm_yupiramos_B123251108_400x300.jpg

Tragen Sie sich kostenfrei im Talentpool auf Controlling-Portal.de ein und erhalten Jobangebote und Unterstützung beim Jobwechsel durch qualifizierte Personalagenturen.

Buch-Vorstellungen


Kennzahlen-Guide

Kennzahlen-Guide-klein.pngÜber 200 Kennzahlen aus Finanzen, Personal, Logistik, Produktion, Einkauf, Vertrieb, eCommerce und IT.
Jede Kennzahl wird in diesem Buch ausführlich erläutert. Neben der Formel wird eine Beispielrechnung aufgeführt. Für viele branchenneutrale Kennzahlen stehen Zielwerte bzw. Orientierungshilfen für eine Bewertung zur Verfügung. Für die genannten Bereiche hat die Redaktion von Controlling-Portal.de jeweils spezialisierte Experten als Autoren gewonnen, die auf dem jeweiligen Gebiet über umfangreiche Praxiserfahrung verfügen. 

Preis: ab 12,90 Euro Brutto  mehr Informationen >>
 

Dashboards mit Excel

dashboards_cover.jpgWie erstelle ich ein Tacho- oder Ampel-Diagramm? Wie kann ich Abweichungen in Tabellen ansprechend visualisieren? Das wird Ihnen hier anschaulich erklärt.

Taschenbuch in Farbe für 34,90 EUR
oder E-Book für 12,90 EUR 
mehr Informationen >>

  

Reporting 1x1

reporting1x1-klein.jpgViel ist zum Berichtswesen oder Reporting schon geschrieben worden. Dennoch zeigen Umfragen, dass rund 50 Prozent der Empfänger von Berichten mit dem Reporting nicht zufrieden sind. Jörgen Erichsen erklärt in diesem Buch die Bedeutung und die Handhabung des Berichtswesens speziell für kleinere Betriebe. Mit zahlreichen Beschreibungen, Beispielen und Checklisten.

Taschenbuch in Farbe für 24,90 EUR
oder E-Book für 15,90 EUR 
mehr Informationen >>

Anzeige

Wie zufrieden sind Sie mit uns?

teamwork_pm_Dmitriy_Shironosov_400x300.jpg  
Über Ihre Meinung und auch ihre Anregungen für Veränderungen oder Erweiterungen würden wir uns sehr freuen. Nur 3 kurze Fragen, die schnell beantwortet sind. Vielen Dank im Voraus für Ihre Mithilfe! zur Umfrage >>

Controlling-Software gesucht?

controlling_Dashboard_pm_ml12nan_B9707546_400x300.jpg

Verschaffen Sie sich hier einen Überblick >>
Facebook_Logo_Primary.png
Bleiben Sie auf dem Laufenden und informieren sich über neue Fachbeiträge, Excel-Tools und Jobangebote auf unserer Facebook-Seite >>

Stellenanzeigen

Buchhalter Immobilien (m/w/d) – Schwerpunkt Mieten- und Objektbuchhaltung
Strohauer ist ein langjährig gewachsenes, familiäres Wohnungsunternehmen mit Immobilienbeständen in Berlin, Hamburg und Dresden. Durch die eigenständige Verwaltung der Immobilien soll ein qualitativ hochwertiges und soziales Arbeiten sichergestellt werden, das den Bestand umsichtig entwickelt. St... Mehr Infos >>

Financial Controller (m/w/d)
Ihre Zukunft – perfekt verpackt. Smurfit Westrock ist der weltweit wegweisende Anbieter von papier­basierten Ver­pack­ungs­lösungen. Mit mehr als 100.000 Mitarbeitenden, 500 Ver­arbei­tungs­betrieben und 63 Fabriken in 40 Ländern bieten wir unseren Kunden eine breite Palette an un­verwechsel­bare... Mehr Infos >>

Leitung Controlling Finanzen (m/w/d)
Sie sind ein analytischer Kopf mit Führungskompetenz und suchen eine Schlüsselposition, in der Sie die Controlling-Strategie eines systemrelevanten, gemeinnützigen Konzerns aktiv prägen, digitalisieren und weiterentwickeln können? Für unser Institut Mannheim suchen wir Sie als Abteilungsleitung C... Mehr Infos >>

Sachbearbeiter*in Buchhaltung in Voll- oder Teilzeit
Wir, das Max-Planck-Institut für medizinische Forschung, sind eines von 85 Instituten und Forschungs­stellen der Max-Planck-Gesell­schaft (MPG) zur Förderung der Wissenschaften e. V. Unser Schwerpunkt liegt in der medizinischen Grundlagen­forschung. Gegenwärtig beschäftigen wir rund 270 M... Mehr Infos >>

Controller strategisches Kapazitätscontrolling (w/m/d)
Hallo, lass uns WIR sagen! Wir - die HUK-COBURG Versicherungsgruppe - zählen zu den 10 größten in Deutschland. Vor über 90 Jahren gegründet sind wir mit über 13 Millionen Kund:innen heute der große Versicherer für Privathaushalte und der größte deutsche Autoversicherer. Dass wir oft preisgünstige... Mehr Infos >>

Controller (m/w/d)
Als traditionsreiches Unternehmen in der Papierindustrie mit klarem Fokus auf Nachhaltigkeit und technologischer Weiterentwicklung, wo seit über 170 Jahren mit rund 300 Mitarbeitenden jährlich ca. 240.000 Tonnen Papier und 80.000 Tonnen grafische Pappe produziert werden, suchen wir zum nächstmögl... Mehr Infos >>

Sachbearbeitung Buchhaltung – „Allround-Talent“ (w/m/d)
Die Verwaltung des Max-Planck-Instituts für extraterrestrische Physik (MPE), des Max-Planck-Instituts für Astrophysik (MPA) und der Max Planck Computing and Data Facility (MPCDF) ist eine zentrale Service­einrichtung und betreut rund 650 Instituts­angehörige. Die gemein­sa... Mehr Infos >>

Controller (m/w/d) für Förder- und Innovationsprojekte
Gestalte mit uns die Zukunft der Halb­leiter­techno­logie und starte Deine Karriere bei Siltronic! Siltronic ist einer der welt­weit größten Her­steller für Wafer aus Reinst­silizium und Partner vieler führender Chip-Her­steller mit rund 4.300 Mitarbeitenden und Pro­duktions­stätten in Europa, As... Mehr Infos >>

Weitere Stellenanzeigen im Stellenmarkt >>

Folgen Sie uns!

panthermedia_B90564160_patronestaff_310px.jpg

Controlling-Portal auf:
Facebook >> und  Linkedin >>

Veranstaltungs-Tipp:
Haufe Online Days - Jahresforum Controlling

Online-Jahresforum-CON_290x100px.jpg
Führende Expertinnen und Experten geben dir Einblicke in die aktuellen Themen, Trends und Entwicklungen im Controlling, wie z.B. KI, Data Intelligence, Strategie und Transformation. Als Teilnehmer:in erwartet dich ein abwechslungsreiches Programm mit Vorträgen, Best Practices, Diskussionen und virtuellem Networking. Freue dich auf wertvolle Impulse, innovative Ideen und konkrete Empfehlungen, um dein Controlling zukunftssicher zu gestalten.   

Erfahre mehr zum Programm >>  

JOB- TIPP

Karriere_290px.png
Sind Sie auf der Suche nach einer neuen Herausforderung? Interessante Stellenangebote für Controller finden Sie in der Controlling-Portal Stellenbörse. Immer auf dem Laufenden bleiben und neue Jobangebote mit dem Jobletter automatisch erhalten? Zur Jobletter-Anmeldung >>

Excel-Tool Plankostenrechnung

Plankostenrechnung mit IST-Abweichung.jpg
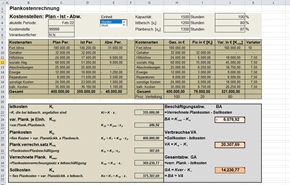
Nach Eingabe der Plankosten und Ist-Kosten für eine Kostenstelle und Periode, sowie der Aufteilung der Kosten in variable und fixe Kosten, werden formelgestützt alle relevanten Größen (Sollkosten, verrechnete Plankosten etc.) ermittelt und eine Abweichungsanalyse (rechnerisch und grafisch) durchgeführt.

Jetzt hier für 25,- EUR downloaden >>

Excel-Tools für Controller!

Diagramme_Charts_pm_chormail@hotmail-com_B347361660_400x300.jpg

Über 500 Vorlagen direkt zum Download. Verschaffen Sie sich einen Überblick >>

Software-Tipps

Lucanet_logo.jpg
LucaNet.Financial Consolidation ist die Software für eine prüfungssichere Konsolidierung, die alle Funktionen für die Erstellung eines legalen Konzernabschlusses nach unterschiedlichen Rechnungslegungsstandards bietet.
Mehr Informationen >>

jedox-logo-250px.jpg
Jedox wird für Planung, Budgetierung, Analyse und Management-Reporting eingesetzt. Dank Excel-naher Benutzeroberfläche und ausgefeilter Dashboard- und Reporting-Funktionen genießt die Lösung eine hohe Akzeptanz im gesamten Unternehmen. Mehr Informationen >>

Weitere Controlling-Software-Lösungen im Marktplatz >>

Projektmanagement-Paket

09_Projektmanagement-Paket.png
Dieses Excel-Vorlagen Paket enthält insgesamt 9 verschiedene Excel-Dateien für die Projektplanung und das Projektmanagement. Alle Dateien sind einfach zu bedienen und können vom Nutzer beliebig angepasst werden.
Mehr Informationen >>


Dokumentenverfolgung mit Excel

In verschiedenen Projekten muss oft eine große Anzahl von Dokumenten termingemäß erstellt und geliefert werden. Dieses Excel-Tool enthält die dazu erforderlichen Tabellenvorlagen sowie die notwendigen Berechnungsmodelle, deren Ergebnisse in einem integrierten Dashboard präsentiert werden. 
Mehr Informationen >>

Bilanzanalyse mit Excel

Das umfangreiche Excel- Tool berechnet die wichtigsten branchenunabhängigen Kennzahlen aus Bilanz und GuV. Neben den Kennzahlen, die mit Erläuterungen versehen sind, werden die G+V und Bilanz in 5 Jahres-Übersicht dargestellt und automatisch eine Kapitalflussrechnung erstellt.
Mehr Informationen >>

Weitere über 400 Excel-Vorlagen finden Sie hier >>
Premium-Mitglied werden

Excel TOP-SellerRS Liquiditätsplanung L

PantherMedia_pannawat_B100513902_400x300.jpg
Die RS Liquiditätsplanung L ist ein in Excel erstelltes Werkzeug für die Liquiditätsplanung von Kleinunternehmen sowie Freiberuflern. Die Planung erfolgt auf Basis von veränderbaren Einnahmen- und Ausgabepositionen. Detailplanungen können auf extra Tabellenblättern für z.B. einzelne Projekte oder Produkte vorgenommen werden. 
Mehr Informationen >>

Rollierende Liquiditätsplanung auf Wochenbasis

Dieses Excel-Tool bietet Ihnen die Grundlage für ein Frühwarnsystem. Der erstellte Liquiditätsplan warnt Sie vor bevorstehenden Zahlungsengpässen, so dass Sie frühzeitig individuelle Maßnahmen zur Liquiditätssicherung einleiten können. Gerade in Krisensituationen ist eine kurzfristige Aktualisierung und damit schnelle Handlungsfähigkeit überlebenswichtig. Mehr Informationen >>

Strategie-Toolbox mit verschiedenen Excel-Vorlagen

Die Strategie-Toolbox enthält 10 nützliche Excel Vorlagen, die sich erfolgreich in der Strategie bewährt haben. Alle Tools sind sofort einsatzbereit und sind ohne Blattschutz. Damit können die Vorlagen individuell angepasst werden.
Ideal für Mitarbeiter aus dem strategischen Management. Mehr Informationen>>

Weitere über 400 Excel-Vorlagen finden Sie hier >>

Software-Tipp

Liquiditätsplanung_Fimovi.jpgRollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. Mehr Infos und Download >>