Yield ist der Zinssatz, zu dem Betrag von vergünstigte Gutscheine und dem abgezinsten Nennwert entspricht dem Marktpreis der Anleihe
Um die Ausbeute zu finden, muss man iterative Methoden wie Newton-Raphson-Methode verwenden, um eine ungefähre Ergebnis zu erhalten
Um Newton-Raphson-Methode erfordert die Definition der Funktion f (i) als Anleihekurs und dann die Differenz f '(i) der Anleihekurs Funktion zu finden
Wir würden eine Vermutung Rate wie z, B, 10% wählen, um die iterative Berechnungen starten, Wenn solche Berechnungen konvergieren dann haben wir eine der Zinsen gefunden zu haben, Die iterative Berechnungen mit einer anderen Vermutung Rate Else starten wir
Abrechnungsdatum (=Emissionsdatum): 15.02.2011
Fälligkeitsdatum: 15.02.2016
Laufzeit in Jahren = 5
Zins (=Kupon): 7,0%
Kurs (Tageskurs): 65,5%
Rückzahlung (=Rückzahungskurs): 100%
Häufigkeit: 1
Rendite entspricht dann: 18,04%
[code]
f(i) = 100 + -65,5 * (1+i)^5 + 7 [(1+i)^5 - 1]/i
f'(i) = 5 * -65,5 * (1+i)^4 + 7 * (5 i (1 + i)^4 - (1 + i)^5 + 1) / (i^2)
i = 0,1
f(i) = 37,2473
f'(i) = -394,4148
i1 = 0,1 - 37,2473/-394,4148 = 0,19443687133912
Fehler Bound = 0,19443687133912 - 0,1 = 0,094437 > 0,000001
i1 = 0,19443687133912
f(i1) = -7,7176
f'(i1) = -565,2016
i2 = 0,19443687133912 - -7,7176/-565,2016 = 0,18078223799448
Fehler Bound = 0,18078223799448 - 0,19443687133912 = 0,013655 > 0,000001
i2 = 0,18078223799448
f(i2) = -0,1887
f'(i2) = -537,7285
i3 = 0,18078223799448 - -0,1887/-537,7285 = 0,18043133175604
Fehler Bound = 0,18043133175604 - 0,18078223799448 = 0,000351 > 0,000001
i3 = 0,18043133175604
f(i3) = -0,0001
f'(i3) = -537,0354
i4 = 0,18043133175604 - -0,0001/-537,0354 = 0,18043110529705
Fehler Bound = 0,18043110529705 - 0,18043133175604 = 0 < 0,000001
Periodenrendite = 18,04%
[/code]
Abrechnungsdatum (=Emissionsdatum): 20.10.2011
Fälligkeitsdatum: 15.02.2016
Laufzeit in Jahren = 4,31944444444444444444444444444444
Zins (=Kupon): 7,0%
Kurs (Tageskurs): 65,5%
Rückzahlung (=Rückzahungskurs): 100%
Häufigkeit: 1
Rendite entspricht dann: 19,55%
[code]
f(i) = 100 + -65,5 * (1+i)^4,3194444444444 + 7 [(1+i)^4,3194444444444 - 1]/i
f'(i) = 4,3194444444444 * -65,5 * (1+i)^3,3194444444444 + 7 * (4,3194444444444 i (1 + i)^3,3194444444444 - (1 + i)^4,3194444444444 + 1) / (i^2)
i = 0,1
f(i) = 36,7921
f'(i) = -329,8823
i1 = 0,1 - 36,7921/-329,8823 = 0,21153108968811
Fehler Bound = 0,21153108968811 - 0,1 = 0,111531 > 0,000001
i1 = 0,21153108968811
f(i1) = -7,3274
f'(i1) = -466,5798
i2 = 0,21153108968811 - -7,3274/-466,5798 = 0,19582669536291
Fehler Bound = 0,19582669536291 - 0,21153108968811 = 0,015704 > 0,000001
i2 = 0,19582669536291
f(i2) = -0,1674
f'(i2) = -445,3774
i3 = 0,19582669536291 - -0,1674/-445,3774 = 0,19545093068852
Fehler Bound = 0,19545093068852 - 0,19582669536291 = 0,000376 > 0,000001
i3 = 0,19545093068852
f(i3) = -0,0001
f'(i3) = -444,8782
i4 = 0,19545093068852 - -0,0001/-444,8782 = 0,19545071984646
Fehler Bound = 0,19545071984646 - 0,19545093068852 = 0 < 0,000001
Periodenrendite = 19,55%
[/code]


















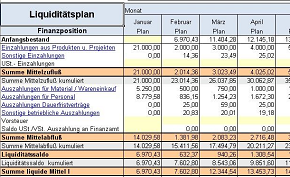

 Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen.
Rollierende Liquiditätsplanung auf Wochenbasis. Mit der Excel-Vorlage „Liquiditätstool“ erstellen Sie schnell und einfach ein Bild ihrer operativen Liquiditätslage für die nächsten (bis zu 52) Wochen. 